Introduction – How can I get insight into my data?
Our daily life brings us tons of data. Our smartphones, a collection of ten sensors or even more, follow us everywhere we go to. Another example is our credit or debit card account. Everytime we pay, we leave an entry in the record. Depending upon the business we work in, there are much more opportunities for data aggregation. Among others, these are:
- Measurements
- Calculations
- Simulations
- Daily business, such as
- Access to website
- Customer data (country, region, zip code, sales volume, branch, etc.)
- Weather forecast
- Utilisation of servers, vehicles, tools, etc.
- Accounting, stock market, etc.
I would like to show an easy way to understand data, to analyse the past, and to find trends for the future. However, I do not like to employ spreadsheets for this task, since data wrangling with cells and clicks is tedious and prone to errors.
Data Analysis – How do I analyse my data efficiently?
There are several approaches for data analysis. Beside spreadsheets, there are several scripting languages which are famous for their statistics features, such as R and S. However, the language Python is more convenient as it is not restricted to statistics but an universal programming language allowing coding of almost all tasks from a simple calculator until a web server. The primary focus of their developers is easy readability, which is the reason why people sometimes say that Python is executable pseudo-code. Moreover, it is open-source and extendible with modules. Here, we would like to employ:
- pandas
- NumPy
- matplotlib
Most of the features we will use here are taken from pandas. This module has been developed for the analysis of time series for stock market and provides data frames with tabular structure allowing access to rows, columns, and cells. The installation routine of Python and the modules depend upon the operating system. There is an excellent documentation tackling this task: https://pandas.pydata.org/pandas-docs/stable/install.html. For further reading, checkout the PyData website (https://pandas.pydata.org).
Our script-based approach features some important advantages:
- Few commands only
- Less error prone than manual spreadsheet work
- Very efficient
Let’s get started. At the beginning we have to import the required modules.
In [1]:
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as pltExample: Black-box of a thermo-hydraulic system
Story
We have a thermo-hydraulic system without any knowledge of its internal structure. Therefore, we plug it into a test bench, connect supply and return of water, and the electrical power cable. Moreover, we measure a couple of quantities, such as:
- Flow rate Q
- Pressure difference between inlet and outlet Δp
- Temperatures of inlet T1 and outlet T2
- Electrical power P
Scheme for a black-box thermohydraulic system
In order to acquire operation data of the system, the following work flow is carried out:
- Adjusting the flow rate to the desired value
- Waiting until steady state
- Measuring the physical quantities
- Storing data into CSV file
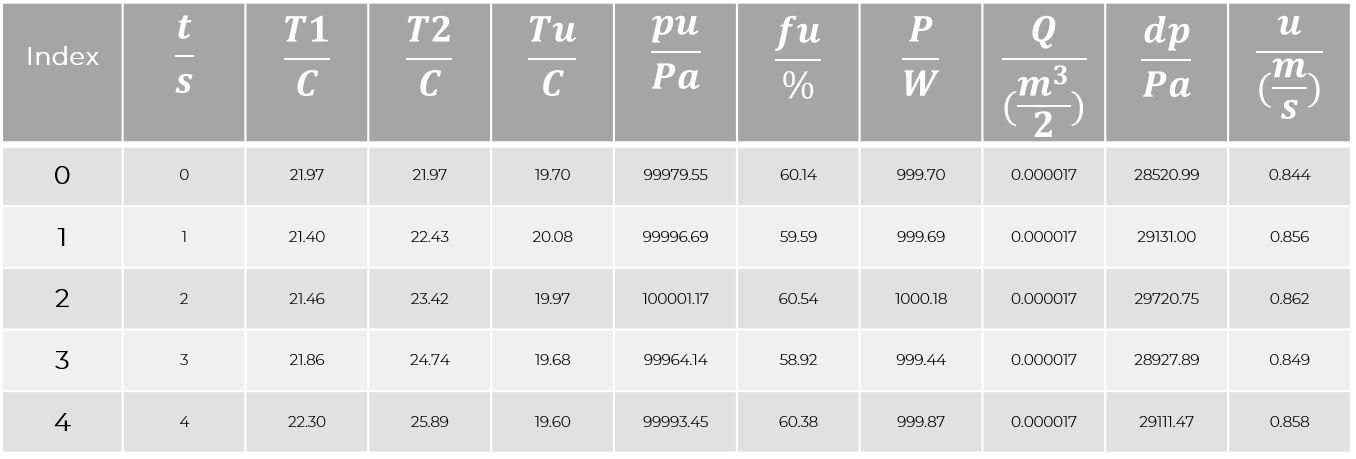
Reading data from a CSV file
The data is stored in a CSV file that actually uses spaces as column separators. Loading a file and creating a data frame df is as easy as:
In [2]:
df = pd.read_csv('measurement_1.csv', sep=' ')A data frame is an indexed matrix-like structure with entries that can be addressed with their row (index) and column (title).
What is stored in the data frame?
There are several options to list the entities stored in a data frame. These are:
- df: showing all entries (for large data sets, the beginning and end only)
- df.head(): showing the first 5 rows (any other value can be provided as argument)
- df.tail(): showing the last 5 rows (any other value can be provided as argument)
In [3]:
df.head()Out[3]:
N.b.: The table head is determined automatically from the CSV file. It could have been also redefined in the pd.read_csv() command.
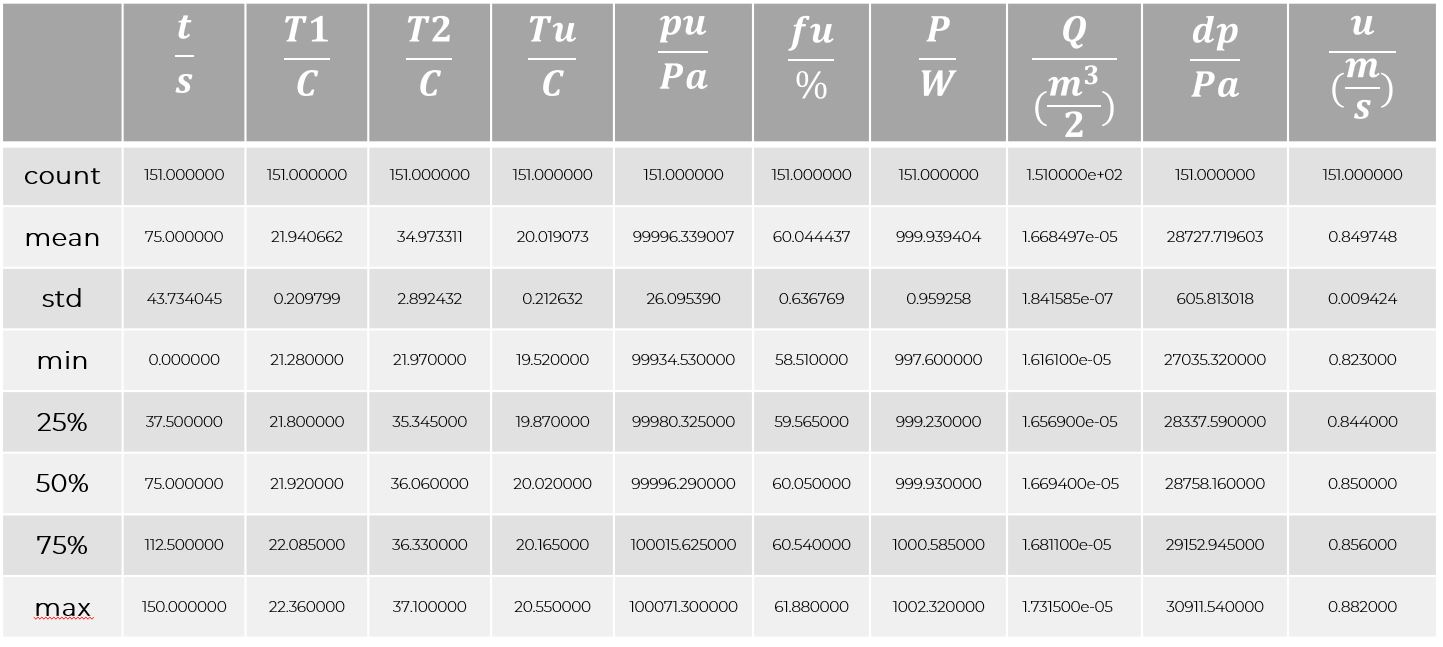
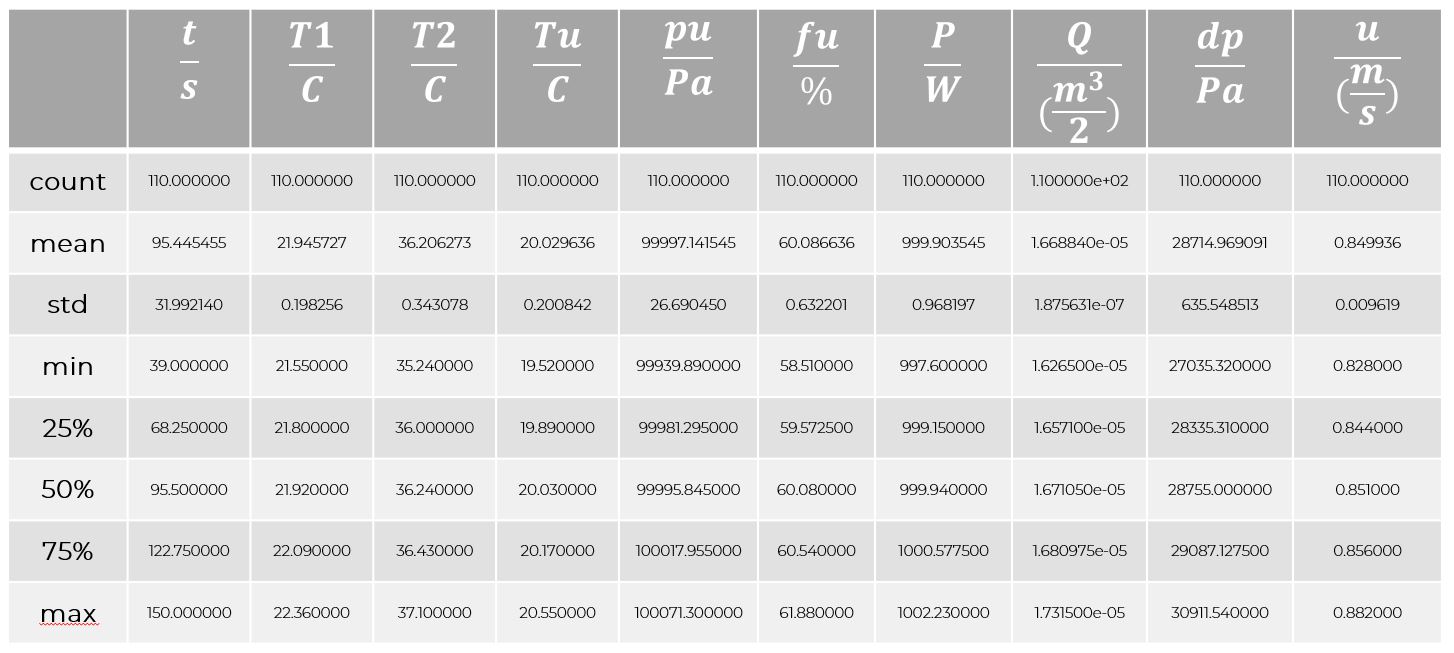
How do I get the full statistics?
The statistics of a data frame can be easily obtained by calling the method describe(). This provides the number of valid entries, i.e., non-NaN values, the mean value, the standard deviation, and various quantiles of the sample of each column. By the way, the method describe() can also be applied to non-numeric columns, where the number of entries is returned.
In [4]:
df.describe()Out[4]:
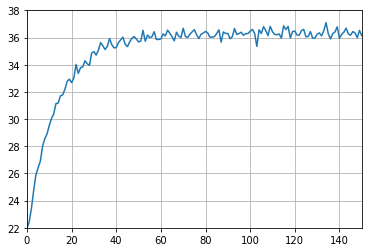
How do I plot data of a particular column?
Reading data in a tabulated manner is very often not intuitive. For this purpose, the plot() method of a data frame can be employed. Here, we would like to see the evolution of the temperature T2 over time within the limits of [22,38] and save the resulting figure to a PDF file. The figure file type can be also any other common one, such as (E)PS, PNG, JPG, etc.
In [5]:
df['T2/C'].plot(grid=True, ylim=(22,38))
plt.savefig('t2.pdf')
How do I find the steady-state?
Calculating the running mean value
The next step in our analysis is to consider the data only when the system is in a steady-state, i.e., the thermodynamic quantities do not vary more than the noise of the signal. For this purpose, we evaluate the mean value of a particular time interval just before the time under consideration. This feature is implemented with the method rolling() which accepts several arguments. Here we define the length to be 20 entries and the minimum length to be 20, too. This is important for the behaviour at the beginning. Just try on your own, what happens if you set min_periods to other values. Afterwards, the method mean() is applied, which calculates the mean value of all quantities in this interval. The results are stored in a new data frame dff.
In [6]:
dff=df['T2/C'].rolling(20,min_periods=20).mean()The following plot shows that the first 20 entries (0…19 s) are without data, which is not quite surprising as the default behaviour of the method rolling() is to store its value at the end of the interval. It can be observed that the running mean is more or less constant from times greater than 70 s in this particular example. However, we do not know this a priori.
In [7]:
dff.plot(grid=True, ylim=(22,38))
Calculating with columns
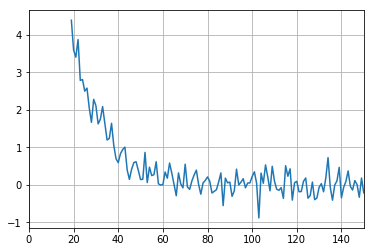
Now, we want to use the running mean data frame dff for determining the data when the system is in steady-state. Therefore, we calculate the difference of the present temperature and its running mean value. We see that the difference is less than 1 K for most of the values from times greater than 40 s.
In [8]:
diff=(df['T2/C']-dff)
diff.plot(grid=True)
plt.savefig('t2_diff.pdf')Evolution of the temperature difference between the outlet temperature and the coinciding running mean value
Creating a filter
We can now create a filter that stores the result of an inequality as a Boolean array. Here, we check if the temperature difference is less than 2.5% of the coinciding temperature. Again, there is no output, since the result is assigned to a variable.
In [9]:
fil = diff < 0.025*df['T2/C']The output of the filter variable fil is the Boolean array. It can be observed that the first and the last thirty entries are shown in order to keep the list comprehensible.
In [10]:
filOut[10]:
0 False
1 False
2 False
3 False
4 False
5 False
6 False
7 False
8 False
9 False
10 False
[40 lines more]
141 True
142 True
143 True
144 True
145 True
146 True
147 True
148 True
149 True
150 True
Name: T2/C, Length: 151, dtype: boolUsing filtered values only
The filter fil can be applied to the original data frame df by employing the squared bracket. The method describe() reveals the statistics of the filtered data frame, i.e., only of those rows for which the filter is true. Compared to Out[5] we see that roughly 40 data points are not considered. Thus, the mean value of T2/C is now slightly higher.
In [11]:
df[fil].describe()Out[11]:
If not the entire statistics is required, but some particular values only, they can be addressed with the methods min(), max(), mean(), std(), median() and quantile(x), where $xin[0,1]$. Here, the mean values are calculated as follows:
In [12]:
df[fil].mean()Out[12]:
t/s 95.445455
T1/C 21.945727
T2/C 36.206273
Tu/C 20.029636
pu/Pa 99997.141545
fu/% 60.086636
P/W 999.903545
Q/(m^3/s) 0.000017
dp/Pa 28714.969091
u/(m/s) 0.849936
dtype: float64
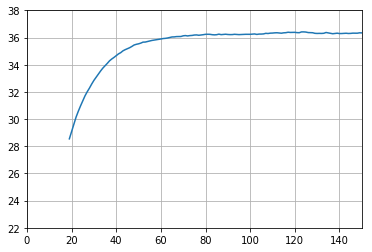
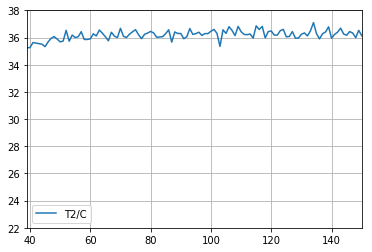
Finalising th e analysis, we plot the temperature T2 for the filtered values only. We can see that temperature indeed is quite constant, besides of the noise.
In [13]:
df.loc[fil,['T2/C']].plot(grid=True, ylim=(22,38))
plt.savefig('t2_filtered.pdf')Evolution of the outlet temperature; filtered to steady-state conditions
Summary – What have we learned?
Summarising this post, we can make the following statements:
- Data analysis is easy and very efficient with Python and pandas.
- Matplotlib is a convenient tool to produce nice figures.
- Results can easily be exportet to HTML, PDF and other formats.
Therefore, I strongly advice to give Python + pandas a try and start today!
#Python #PyData #DataAnalysis #pandas #futureofcompute @cloudandheat https://cloudandheat.com